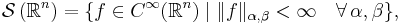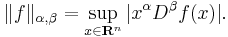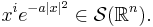Schwartz space

For the Schwartz space of a semisimple Lie group, see Harish-Chandra's Schwartz space.

In mathematics, Schwartz space is the function space of functions all of whose derivatives are rapidly decreasing. This space has the important property that the Fourier transform is an automorphism on this space. This property enables one, by duality, to define the Fourier transform for elements in the dual space of $\mathcal{S}$ , that is, for tempered distributions. Schwartz space is named in honour of Laurent Schwartz. A function in the Schwartz space is sometimes called a Schwartz function.

1 Definition
2 Examples of functions in S
3 Properties
4 References

Definition

The Schwartz space or space of rapidly decreasing functions 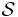$\mathcal{S}$ on Rⁿ is the function space

$\mathcal{S} \left(\mathbb{R}^n\right) = \{ f \in C^\infty(\mathbb{R}^n) \mid \|f\|_{\alpha,\beta} < \infty\quad \forall \, \alpha, \beta \},$

where α, β are multi-indices, C^∞(Rⁿ) is the set of smooth functions from Rⁿ to C, and

$\|f\|_{\alpha,\beta}=\sup_{x\in\mathbf{R}^n}|x^\alpha D^\beta f(x)|.$

Here, sup denotes the supremum, and we again use multi-index notation. When the dimension n is clear, it is convenient to write 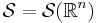$\mathcal{S}=\mathcal{S}(\mathbb{R}^n)$ .

To put common language to this definition, we could note that a rapidly decreasing function is essentially a function f(x) such that f(x), f'(x), f''(x), ... all exist everywhere on the real line and go to zero as 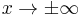$x \to \pm \infty$ faster than any inverse power of x. Especially, 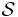$\mathcal{S}$ is a subspace of the function space 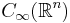$C_{\infty}(\mathbb{R}^n)$ of continuous functions which vanish at infinity.

Examples of functions in S

If i is a multi-index, and a is a positive real number, then

$x^i e^{-a |x|^2} \in \mathcal{S} (\mathbb{R}^n).$

Any smooth function f with compact support is in 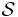$\mathcal{S}$ . This is clear since any derivative of f is continuous and supported in the support of f, so (x^α D^β) f has a maximum in Rⁿ by the extreme value theorem.

Properties

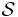$\mathcal{S}$ is a Fréchet space over the complex numbers.

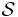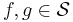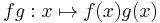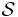Using Leibniz' rule, it follows that $\mathcal{S}$ is also closed under point-wise multiplication; if $f,g \in \mathcal{S}$ , then $fg: x\mapsto f(x)g(x)$ is also in $\mathcal{S}$ .

For any 1 ≤ p ≤ ∞, we have 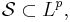$\mathcal{S}\subset L^p,$ where L^p(Rⁿ) is the space of p-integrable functions on Rⁿ.

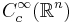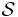The space of all bump functions, $C^\infty_c({\Bbb R}^n)$ , is included in $\mathcal{S}$ .

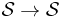The Fourier transform is a linear isomorphism $\mathcal{S} \to \mathcal{S}$ .

If 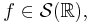$f \in \mathcal{S}(\mathbb{R}),$ then $f$ is uniformly continuous on $\mathbb{R}$ .

References

Hörmander, L. (1990). The Analysis of Linear Partial Differential Operators I, (Distribution theory and Fourier Analysis) (2nd ed.). Berlin: Springer-Verlag. ISBN 354052343X.
Reed, M.; Simon, B. (1980). Methods of Modern Mathematical Physics: Functional Analysis I (Revised and enlarged ed.). San Diego: Academic Press. ISBN 0125850506.
Stein, Elias M.; Shakarchi, Rami (2003). Fourier Analysis: An Introduction (Princeton Lectures in Analysis I<). Princeton: Princeton University Press. ISBN 069111384X.

This article incorporates material from Space of rapidly decreasing functions on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

Schwartz space

Contents

Definition

Examples of functions in S

Properties

References